Satoshiego Nakamoto
satoshin@gmx.com
www.bitcoin.org

Streszczenie: Wersja elektronicznej gotówki typu peer-to-peer umożliwiłaby przesyłanie płatności online bezpośrednio od jednej strony do drugiej, bez konieczności przechodzenia przez instytucję finansową. Podpisy cyfrowe stanowią część rozwiązania, ale główne korzyści zostaną utracone, jeśli w celu zapobiegania podwójnym wydatkom nadal wymagana będzie zaufana strona trzecia. Proponujemy rozwiązanie problemu podwójnych wydatków za pomocą sieci peer-to-peer. Sieć oznacza transakcje znacznikami czasu, mieszając je w ciągły łańcuch dowodów pracy opartych na skrótach, tworząc zapis, którego nie można zmienić bez ponownego wykonania dowodu pracy. Najdłuższy łańcuch służy nie tylko jako dowód sekwencji obserwowanych zdarzeń, ale także jako dowód, że pochodzi z największej puli mocy procesora. Dopóki większość mocy procesora jest kontrolowana przez węzły, które nie współpracują w celu ataku na sieć, będą one generować najdłuższy łańcuch i wyprzedzić atakujących. Sama sieć wymaga minimalnej struktury. Wiadomości są transmitowane przy zachowaniu najwyższej staranności, a węzły mogą według własnego uznania opuszczać sieć i ponownie do niej dołączać, akceptując najdłuższy łańcuch dowodów pracy jako dowód tego, co wydarzyło się podczas ich nieobecności.
1. Wstęp
Handel w Internecie opiera się niemal wyłącznie na instytucjach finansowych pełniących rolę zaufanych stron trzecich w zakresie przetwarzania płatności elektronicznych. Chociaż system działa wystarczająco dobrze w przypadku większości transakcji, nadal ma nieodłączne słabości modelu opartego na zaufaniu. Całkowicie nieodwracalne transakcje nie są w rzeczywistości możliwe, ponieważ instytucje finansowe nie mogą uniknąć mediacji w sporach. Koszt mediacji zwiększa koszty transakcji, ograniczając minimalną praktyczną wielkość transakcji i odcinając możliwość małych, przypadkowych transakcji, a większym kosztem jest utrata możliwości dokonywania nieodwracalnych płatności za nieodwracalne usługi. Wraz z możliwością odwrócenia rozprzestrzenia się potrzeba zaufania. Sprzedawcy muszą uważać na swoich klientów i namawiać ich do uzyskania większej ilości informacji, niż byliby potrzebni w innym przypadku. Przyjmuje się, że pewien procent oszustw jest nieunikniony. Tych kosztów i niepewności związanych z płatnościami można uniknąć osobiście, korzystając z waluty fizycznej, nie istnieje jednak mechanizm umożliwiający dokonywanie płatności za pośrednictwem kanału komunikacyjnego bez zaufanej strony.
Potrzebny jest system płatności elektronicznych oparty na dowodzie kryptograficznym, a nie na zaufaniu, umożliwiający dwóm chętnym stronom bezpośrednią transakcję między sobą, bez konieczności korzystania z zaufanej strony trzeciej. Transakcje, których odwrócenie jest niepraktyczne obliczeniowo, chroniłyby sprzedawców przed oszustwami, a w celu ochrony kupujących można łatwo wdrożyć rutynowe mechanizmy depozytowe. W tym artykule proponujemy rozwiązanie problemu podwójnych wydatków przy użyciu rozproszonego serwera znaczników czasu typu peer-to-peer w celu wygenerowania dowodu obliczeniowego chronologicznej kolejności transakcji. System jest bezpieczny, o ile uczciwe węzły wspólnie kontrolują większą moc procesora niż jakakolwiek współpracująca grupa węzłów atakujących.
2. Transakcje
Monetę elektroniczną definiujemy jako łańcuch podpisów cyfrowych. Każdy właściciel przekazuje monetę kolejnemu, podpisując cyfrowo hash poprzedniej transakcji i klucz publiczny kolejnego właściciela i dodając je na końcu monety. Odbiorca może zweryfikować podpisy, aby zweryfikować łańcuch własności.

Problem polega oczywiście na tym, że odbiorca nie może zweryfikować, czy jeden z właścicieli nie wydał dwukrotnie monety. Powszechnym rozwiązaniem jest wprowadzenie zaufanego organu centralnego, czyli mennicy, która sprawdza każdą transakcję pod kątem podwójnych wydatków. Po każdej transakcji monetę należy zwrócić do mennicy w celu wyemitowania nowej, a jedynie monety wyemitowane bezpośrednio z mennicy nie podlegają podwójnemu wydaniu. Problem z tym rozwiązaniem polega na tym, że losy całego systemu pieniężnego zależą od firmy prowadzącej mennicę i każda transakcja musi przez nią przechodzić, zupełnie jak bank. Potrzebujemy sposobu, aby odbiorca wiedział, że poprzedni właściciele nie podpisali żadnych wcześniejszych transakcji. Dla naszych celów liczy się najwcześniejsza transakcja, dlatego nie przejmujemy się późniejszymi próbami podwójnego wydania. Jedynym sposobem potwierdzenia braku transakcji jest zapoznanie się z wszystkimi transakcjami. W modelu menniczym mennica była świadoma wszystkich transakcji i decydowała, która z nich dotarła jako pierwsza. Aby to osiągnąć bez zaufanej strony, transakcje muszą być ogłaszane publicznie [1] i potrzebujemy systemu umożliwiającego uczestnikom uzgodnienie jednej historii kolejności ich otrzymania. Odbiorca potrzebuje dowodu, że w momencie każdej transakcji większość węzłów zgodziła się, że jest to pierwsza otrzymana transakcja.
3. Serwer znacznika czasu
Proponowane przez nas rozwiązanie zaczyna się od serwera znaczników czasu. Serwer znacznika czasu działa poprzez pobieranie skrótu bloku elementów, które mają zostać opatrzone znacznikiem czasu, i szerokie publikowanie skrótu, na przykład w gazecie lub poście w Usenecie [2-5]. Znacznik czasu dowodzi, że dane musiały oczywiście istnieć w danym momencie, aby mogły zostać wprowadzone do skrótu. Każdy znacznik czasu zawiera poprzedni znacznik czasu w swoim hashu, tworząc łańcuch, przy czym każdy dodatkowy znacznik czasu wzmacnia poprzedni.

4. Dowód pracy
Aby zaimplementować rozproszony serwer znaczników czasu na zasadzie peer-to-peer, będziemy musieli użyć systemu dowodu pracy podobnego do Hashcash Adama Backa [6], a nie postów w gazetach lub Usenecie. Dowód pracy polega na skanowaniu wartości, która po zaszyfrowaniu, na przykład w przypadku SHA-256, skrót zaczyna się od pewnej liczby bitów zerowych. Średnia wymagana praca jest wykładnicza pod względem liczby wymaganych bitów zerowych i można ją zweryfikować, wykonując pojedynczy skrót.
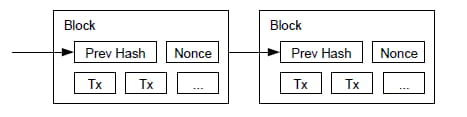
W naszej sieci znaczników czasu implementujemy dowód pracy, zwiększając wartość jednorazową w bloku, aż zostanie znaleziona wartość, która zapewni skrótowi bloku wymagane bity zerowe. Po włożeniu wysiłku procesora w celu spełnienia wymagań dowodu pracy, bloku nie można zmienić bez ponownego wykonania pracy. Ponieważ późniejsze bloki są po nim połączone, praca nad zmianą bloku będzie obejmować ponowne wykonanie wszystkich bloków znajdujących się po nim.
Dowód pracy rozwiązuje również problem określenia reprezentacji w procesie decyzyjnym większości. Gdyby większość opierała się na zasadzie „jeden adres IP – jeden głos”, mogłaby zostać obalona przez każdego, kto jest w stanie przydzielić wiele adresów IP. Dowód pracy to zasadniczo jeden procesor - jeden głos. Decyzja większości jest reprezentowana przez najdłuższy łańcuch, w który włożono najwięcej wysiłku w zakresie dowodu pracy. Jeśli większość mocy procesora jest kontrolowana przez uczciwe węzły, uczciwy łańcuch będzie rósł najszybciej i wyprzedzi wszelkie konkurencyjne łańcuchy. Aby zmodyfikować poprzedni blok, atakujący musiałby ponownie przeprowadzić dowód działania bloku i wszystkich bloków po nim, a następnie dogonić i przewyższyć pracę uczciwych węzłów. Pokażemy później, że prawdopodobieństwo, że wolniejszy atakujący dogoni przeciwnika, maleje wykładniczo w miarę dodawania kolejnych bloków.
Aby zrekompensować rosnącą prędkość sprzętu i zmieniające się z biegiem czasu zainteresowanie uruchamianiem węzłów, trudność dowodu pracy jest określana na podstawie średniej ruchomej określającej średnią liczbę bloków na godzinę. Jeśli są generowane zbyt szybko, trudność wzrasta.
5. Sieć
Aby uruchomić sieć, należy wykonać następujące kroki:
1) Nowe transakcje są transmitowane do wszystkich węzłów.
2) Każdy węzeł gromadzi nowe transakcje w bloku.
3) Każdy węzeł pracuje nad znalezieniem trudnego dowodu działania dla swojego bloku.
4) Kiedy węzeł znajdzie dowód pracy, rozgłasza blok do wszystkich węzłów.
5) Węzły akceptują blok tylko wtedy, gdy wszystkie zawarte w nim transakcje są ważne i nie zostały jeszcze wydane.
6) Węzły wyrażają akceptację bloku pracując nad utworzeniem kolejnego bloku w łańcuchu, używając hasha zaakceptowanego bloku jako hasha poprzedniego.
Węzły zawsze uważają najdłuższy łańcuch za właściwy i będą dalej pracować nad jego wydłużeniem. Jeśli dwa węzły jednocześnie transmitują różne wersje następnego bloku, niektóre węzły mogą najpierw otrzymać jedną lub drugą. W takim przypadku pracują nad pierwszą otrzymaną gałęzią, ale zachowują drugą gałąź na wypadek, gdyby stała się dłuższa. Remis zostanie zerwany, gdy zostanie znaleziony kolejny dowód pracy i jedna gałąź stanie się dłuższa; węzły, które pracowały na drugiej gałęzi, zostaną następnie przełączone na dłuższą.
Nowe transmisje transakcji nie muszą koniecznie docierać do wszystkich węzłów. Dopóki dotrą do wielu węzłów, wkrótce dostaną się do bloku. Transmisje blokowe tolerują także porzucone wiadomości. Jeśli węzeł nie otrzyma bloku, poprosi o niego, gdy odbierze następny blok i zorientuje się, że go przeoczył.
6. Zachęta
Zgodnie z konwencją, pierwsza transakcja w bloku jest specjalną transakcją, która uruchamia nową monetę będącą własnością twórcy bloku. Stanowi to zachętę dla węzłów do obsługi sieci i umożliwia początkową dystrybucję monet do obiegu, ponieważ nie ma organu centralnego, który mógłby je emitować. Stałe dodawanie stałej ilości nowych monet jest analogiczne do sytuacji, w której górnicy złota wydają zasoby, aby dodać złoto do obiegu. W naszym przypadku zużywany jest czas procesora i energia elektryczna.
Motywacja może być również finansowana z opłat transakcyjnych. Jeżeli wartość wyjściowa transakcji jest mniejsza niż jej wartość wejściowa, różnica stanowi opłatę transakcyjną doliczaną do wartości motywacyjnej bloku zawierającego transakcję. Po wejściu do obiegu określonej liczby monet zachęta może całkowicie przekształcić się w opłaty transakcyjne i być całkowicie wolna od inflacji.
Zachęta może zachęcić węzły do zachowania uczciwości. Jeśli chciwy atakujący będzie w stanie zgromadzić więcej mocy procesora niż wszystkie uczciwe węzły, będzie musiał wybrać pomiędzy wykorzystaniem jej do oszukiwania ludzi poprzez kradzież płatności lub wykorzystaniem jej do generowania nowych monet. Powinien uznać za bardziej opłacalne przestrzeganie zasad, takich zasad, które faworyzują go większą liczbą nowych monet niż wszyscy inni razem wzięci, niż podważanie systemu i ważności jego własnego bogactwa.
7. Odzyskiwanie miejsca na dysku
Gdy ostatnia transakcja na monecie zostanie ukryta pod wystarczającą liczbą bloków, wydane przed nią transakcje można odrzucić, aby zaoszczędzić miejsce na dysku. Aby to ułatwić bez naruszania skrótu bloku, transakcje są szyfrowane w drzewie Merkle [7] [2] [5], przy czym w haszu bloku zawarty jest tylko korzeń. Stare bloki można następnie zagęścić, odcinając gałęzie drzewa. Wewnętrzne skróty nie muszą być przechowywane.

Nagłówek bloku bez transakcji miałby około 80 bajtów. Jeśli założymy, że bloki są generowane co 10 minut, 80 bajtów 6 24 * 365 = 4,2 MB rocznie. Ponieważ od 2008 r. systemy komputerowe były zwykle sprzedawane z 2 GB pamięci RAM, a prawo Moore'a przewidywało bieżący wzrost o 1,2 GB rocznie, przechowywanie nie powinno stanowić problemu, nawet jeśli nagłówki bloków muszą być przechowywane w pamięci.
8. Uproszczona weryfikacja płatności
Istnieje możliwość weryfikacji płatności bez konieczności uruchamiania pełnego węzła sieci. Użytkownik musi jedynie zachować kopię nagłówków bloków najdłuższego łańcucha dowodu pracy, którą może uzyskać, wysyłając zapytania do węzłów sieci, dopóki nie będzie przekonany, że ma najdłuższy łańcuch, i uzyskać gałąź Merkle łączącą transakcję z blokiem jest oznaczony znacznikiem czasu. Nie może sam sprawdzić transakcji, ale łącząc ją z miejscem w łańcuchu, może zobaczyć, że węzeł sieci ją zaakceptował, a dodane po niej blokady dodatkowo potwierdzają, że sieć ją zaakceptowała.

W związku z tym weryfikacja jest niezawodna, o ile uczciwe węzły kontrolują sieć, ale jest bardziej podatna na ataki, jeśli sieć zostanie pokonana przez osobę atakującą. Chociaż węzły sieci mogą samodzielnie weryfikować transakcje, uproszczoną metodę można oszukać w wyniku sfabrykowanych transakcji przez osobę atakującą, dopóki osoba atakująca będzie mogła nadal przejmować kontrolę nad siecią. Jedną ze strategii zabezpieczenia się przed tym byłoby akceptowanie alertów z węzłów sieci, gdy wykryją one nieprawidłowy blok, co spowoduje, że oprogramowanie użytkownika pobierze pełny blok i zaalarmuje transakcje w celu potwierdzenia niespójności. Firmy otrzymujące częste płatności prawdopodobnie nadal będą chciały uruchamiać własne węzły w celu zapewnienia bardziej niezależnego bezpieczeństwa i szybszej weryfikacji.
9. Łączenie i dzielenie wartości
Chociaż możliwa byłaby indywidualna obsługa monet, niewygodne byłoby dokonywanie osobnej transakcji dla każdego centa w przelewie. Aby umożliwić dzielenie i łączenie wartości, transakcje zawierają wiele wejść i wyjść. Zwykle będzie to albo pojedynczy wkład z poprzedniej większej transakcji, albo wiele danych wejściowych łączących mniejsze kwoty i co najwyżej dwa wyjścia: jedno dotyczące płatności i drugie zwracające resztę, jeśli taka istnieje, z powrotem do nadawcy.

Warto zaznaczyć, że fan-out, czyli sytuacja, w której transakcja jest uzależniona od kilku transakcji, a te transakcje zależą od znacznie większej liczby transakcji, nie stanowi tutaj problemu. Nigdy nie ma potrzeby wyodrębniania kompletnej, samodzielnej kopii historii transakcji.
10. Prywatność
Tradycyjny model bankowości osiąga poziom prywatności poprzez ograniczenie dostępu do informacji do zaangażowanych stron i zaufanej strony trzeciej. Konieczność ogłaszania wszystkich transakcji publicznie wyklucza tę metodę, ale prywatność można nadal zachować przerywając przepływ informacji w inne miejsce: zachowując anonimowość kluczy publicznych. Opinia publiczna może zobaczyć, że ktoś wysyła kwotę komuś innemu, ale bez informacji łączących transakcję z kimkolwiek. Jest to podobne do poziomu informacji udostępnianych przez giełdy, gdzie czas i wielkość poszczególnych transakcji, czyli „taśma”, są podawane do wiadomości publicznej, ale bez wskazania stron.

Jako dodatkową zaporę ogniową, dla każdej transakcji należy zastosować nową parę kluczy, aby zapobiec powiązaniu ich ze wspólnym właścicielem. Pewne powiązania są nadal nieuniknione w przypadku transakcji z wieloma danymi wejściowymi, które z konieczności ujawniają, że ich dane wejściowe należały do tego samego właściciela. Ryzyko polega na tym, że w przypadku ujawnienia właściciela klucza powiązanie może ujawnić inne transakcje należące do tego samego właściciela.
11. Obliczenia
Rozważamy scenariusz, w którym atakujący próbuje wygenerować alternatywny łańcuch szybciej niż uczciwy łańcuch. Nawet jeśli uda się to osiągnąć, nie naraża to systemu na arbitralne zmiany, takie jak tworzenie wartości z powietrza lub zabieranie pieniędzy, które nigdy nie należały do atakującego. Węzły nie zaakceptują nieprawidłowej transakcji jako płatności, a uczciwe węzły nigdy nie zaakceptują bloku zawierającego je. Osoba atakująca może jedynie spróbować zmienić jedną ze swoich transakcji, aby odzyskać niedawno wydane pieniądze. Wyścig pomiędzy uczciwym łańcuchem a łańcuchem atakujących można scharakteryzować jako dwumianowy spacer losowy. Zdarzeniem sukcesu jest przedłużenie uczciwego łańcucha o jeden blok, zwiększając jego przewagę o +1, a zdarzeniem niepowodzenia jest przedłużenie łańcucha atakującego o jeden blok, zmniejszając różnicę o -1.
Prawdopodobieństwo, że atakujący nadrobi dany deficyt, jest analogiczne do problemu Ruiny Hazardzisty. Załóżmy, że hazardzista z nieograniczonym kredytem zaczyna od deficytu i rozgrywa potencjalnie nieskończoną liczbę prób, próbując osiągnąć próg rentowności. Prawdopodobieństwo, że kiedykolwiek osiągnie próg rentowności lub że atakujący kiedykolwiek dogoni uczciwy łańcuch, możemy obliczyć w następujący sposób [8]:
p = prawdopodobieństwo, że uczciwy węzeł znajdzie następny blok
q = prawdopodobieństwo, że atakujący znajdzie następny blok
qz = prawdopodobieństwo, że atakujący kiedykolwiek dogoni z bloków z tyłu
qz= { 1 jeśli p≤q
(q/ p)^z jeśli p>q}
Biorąc pod uwagę nasze założenie, że p > q, prawdopodobieństwo spada wykładniczo wraz ze wzrostem liczby bloków, które atakujący musi nadrobić. Biorąc pod uwagę jego szanse, jeśli nie uda mu się wcześnie rzucić do przodu, jego szanse staną się znikomo małe, gdy pozostanie w tyle.
Rozważamy teraz, jak długo odbiorca nowej transakcji musi czekać, zanim będzie miał wystarczającą pewność, że nadawca nie może zmienić transakcji. Zakładamy, że nadawca jest atakującym, który chce przez pewien czas sprawić, by odbiorca uwierzył, że mu zapłacił, a następnie zmienić to tak, aby po pewnym czasie zwrócić sobie pieniądze. Odbiorca zostanie o tym powiadomiony, gdy to nastąpi, ale nadawca ma nadzieję, że będzie już za późno.
Odbiorca generuje nową parę kluczy i przekazuje klucz publiczny nadawcy na krótko przed podpisaniem. Uniemożliwia to nadawcy przygotowanie łańcucha bloków z wyprzedzeniem poprzez ciągłą pracę nad nim, dopóki nie uda mu się dotrzeć wystarczająco daleko do przodu, a następnie wykonanie transakcji w tym momencie. Po wysłaniu transakcji nieuczciwy nadawca rozpoczyna w tajemnicy pracę nad równoległym łańcuchem zawierającym alternatywną wersję jego transakcji.
Odbiorca czeka, aż transakcja zostanie dodana do bloku, a po niej zostanie połączonych z bloków. Nie zna dokładnego postępu poczynionego przez atakującego, ale zakładając, że uczciwe bloki zajmowały średni oczekiwany czas na blok, potencjalny postęp atakującego będzie rozkładem Poissona z wartością oczekiwaną:

Konwersja do kodu C...

Analizując pewne wyniki, możemy zobaczyć, że prawdopodobieństwo spada wykładniczo wraz ze wzrostem z.
q=0,1
z=0 P=1,0000000
z=1 P=0,2045873
z=2 P=0,0509779
z=3 P=0,0131722
z=4 P=0,0034552
z=5 P=0,0009137
z=6 P=0,0002428
z=7 P=0,0000647
z=8 P=0,0000173
z=9 P=0,0000046
z=10 P=0,0000012
q=0,3
z=0 P=1,0000000
z=5 P=0,1773523
z=10 P=0,0416605
z=15 P=0,0101008
z=20 P=0,0024804
z=25 P=0,0006132
z=30 P=0,0001522
z=35 P=0,0000379
z=40 P=0,0000095
z=45 P=0,0000024
z=50 P=0,0000006
Rozwiązanie dla P mniejszego niż 0,1%...
P < 0,001
q=0,10 z=5
q=0,15 z=8
q=0,20 z=11
q=0,25 z=15
q=0,30 z=24
q=0,35 z=41
q=0,40 z=89
q=0,45 z=340
12. Wniosek
Zaproponowaliśmy system transakcji elektronicznych bez polegania na zaufaniu. Zaczęliśmy od zwykłego systemu monet wykonanych na podstawie podpisów cyfrowych, który zapewnia silną kontrolę własności, ale jest niekompletny bez sposobu zapobiegania podwójnym wydatkom. Aby rozwiązać ten problem, zaproponowaliśmy sieć peer-to-peer wykorzystującą dowód pracy do rejestrowania publicznej historii transakcji, której zmiana szybko staje się niepraktyczna obliczeniowo dla atakującego, jeśli uczciwe węzły kontrolują większość mocy procesora. Sieć jest solidna w swojej nieustrukturyzowanej prostocie. Węzły działają jednocześnie, przy niewielkiej koordynacji. Nie trzeba ich identyfikować, ponieważ wiadomości nie są kierowane do żadnego konkretnego miejsca i należy je jedynie dostarczyć przy zachowaniu najwyższej staranności. Węzły mogą dowolnie opuszczać sieć i przyłączać się do niej ponownie, akceptując łańcuch dowodu pracy jako dowód tego, co wydarzyło się podczas ich nieobecności. Głosują mocą procesora, wyrażając akceptację ważnych bloków, pracując nad ich rozszerzeniem i odrzucając nieprawidłowe bloki, odmawiając nad nimi pracy. Za pomocą tego mechanizmu konsensusu można egzekwować wszelkie potrzebne zasady i zachęty.
Bibliografia
[1] W. Dai, „b-money”, http://www.weidai.com/bmoney.txt, 1998.
[2] H. Massias, X.S. Avila i J.-J. Quisquater, „Projekt bezpiecznej usługi znakowania czasem przy minimalnym
wymogi zaufania”, podczas 20. Sympozjum Teorii Informacji w krajach Beneluksu, maj 1999.
[3] S. Haber, W.S. Stornetta, „Jak oznaczyć dokument cyfrowy znacznikiem czasu”, w: Journal of Cryptology, tom 3, nie
2, strony 99-111, 1991.
[4] D. Bayer, S. Haber, W.S. Stornetta, „Poprawa wydajności i niezawodności cyfrowego znakowania czasem”,
W sekwencjach II: Metody komunikacji, bezpieczeństwa i informatyki, strony 329–334, 1993.
[5] S. Haber, W.S. Stornetta, „Bezpieczne nazwy ciągów bitowych”, w materiałach z 4. konferencji ACM
w sprawie bezpieczeństwa komputerów i komunikacji, strony 28–35, kwiecień 1997.
[6] A. Back, „Hashcash – środek zaradczy przeciwko odmowie usługi”,
http://www.hashcash.org/papers/hashcash.pdf, 2002.
[7] RC Merkle, „Protokoły dla kryptosystemów klucza publicznego”, w Proc. Sympozjum na temat bezpieczeństwa i 1980 r
Prywatność, IEEE Computer Society, strony 122–133, kwiecień 1980.
[8] W. Feller, „Wprowadzenie do teorii prawdopodobieństwa i jej zastosowań”, 1957.



