Satoshi Nakamoto
satoshin@gmx.com
www.bitcoin.org

Resumen: Una versión puramente peer-to-peer del efectivo electrónico permitiría enviar pagos en línea directamente de una parte a otra sin pasar por una institución financiera. Las firmas digitales proporcionan parte de la solución, pero los principales beneficios se pierden si aún se requiere un tercero confiable para evitar el doble gasto. Proponemos una solución al problema del doble gasto utilizando una red peer-to-peer. La red marca las transacciones mediante hash en una cadena continua de prueba de trabajo basada en hash, formando un registro que no se puede cambiar sin rehacer la prueba de trabajo. La cadena más larga no sólo sirve como prueba de la secuencia de eventos presenciados, sino también como prueba de que provino del mayor conjunto de potencia de CPU. Mientras la mayor parte de la potencia de la CPU esté controlada por nodos que no cooperen para atacar la red, generarán la cadena más larga y superarán a los atacantes. La red en sí requiere una estructura mínima. Los mensajes se transmiten con el mejor esfuerzo y los nodos pueden salir y volver a unirse a la red a voluntad, aceptando la cadena de prueba de trabajo más larga como prueba de lo que sucedió mientras estaban fuera.
1. Introducción
El comercio en Internet ha llegado a depender casi exclusivamente de instituciones financieras que actúan como terceros confiables para procesar pagos electrónicos. Si bien el sistema funciona bastante bien para la mayoría de las transacciones, todavía adolece de las debilidades inherentes del modelo basado en la confianza. Realmente no son posibles transacciones completamente irreversibles, ya que las instituciones financieras no pueden evitar mediar en las disputas. El costo de la mediación aumenta los costos de transacción, limita el tamaño mínimo práctico de la transacción y elimina la posibilidad de pequeñas transacciones casuales, y hay un costo más amplio en la pérdida de la capacidad de realizar pagos no reversibles por servicios no reversibles. Ante la posibilidad de reversión, se extiende la necesidad de confianza. Los comerciantes deben desconfiar de sus clientes y presionarlos para obtener más información de la que de otro modo necesitarían. Se acepta como inevitable un cierto porcentaje de fraude. Estos costos e incertidumbres en los pagos se pueden evitar en persona mediante el uso de moneda física, pero no existe ningún mecanismo para realizar pagos a través de un canal de comunicaciones sin una parte confiable.
Lo que se necesita es un sistema de pago electrónico basado en pruebas criptográficas en lugar de confianza, que permita a dos partes interesadas realizar transacciones directamente entre sí sin la necesidad de un tercero de confianza. Las transacciones que desde el punto de vista computacional no son prácticas de revertir protegerían a los vendedores del fraude, y se podrían implementar fácilmente mecanismos rutinarios de depósito en garantía para proteger a los compradores. En este artículo, proponemos una solución al problema del doble gasto utilizando un servidor de marca de tiempo distribuido punto a punto para generar pruebas computacionales del orden cronológico de las transacciones. El sistema es seguro siempre que los nodos honestos controlen colectivamente más potencia de CPU que cualquier grupo cooperante de nodos atacantes.
2. Transacciones
Definimos una moneda electrónica como una cadena de firmas digitales. Cada propietario transfiere la moneda al siguiente firmando digitalmente un hash de la transacción anterior y la clave pública del siguiente propietario y agregándolos al final de la moneda. Un beneficiario puede verificar las firmas para verificar la cadena de propiedad.

El problema, por supuesto, es que el beneficiario no puede verificar que uno de los propietarios no gastó dos veces la moneda. Una solución común es introducir una autoridad central confiable, o menta, que verifique cada transacción para detectar doble gasto. Después de cada transacción, la moneda debe devolverse a la casa de la moneda para emitir una nueva moneda, y solo se confía en que las monedas emitidas directamente desde la casa de la moneda no se gasten dos veces. El problema con esta solución es que el destino de todo el sistema monetario depende de la empresa que gestiona la casa de moneda, y cada transacción tiene que pasar por ella, como un banco. Necesitamos una forma para que el beneficiario sepa que los propietarios anteriores no firmaron ninguna transacción anterior. Para nuestros propósitos, la transacción más temprana es la que cuenta, por lo que no nos importan los intentos posteriores de realizar doble gasto. La única forma de confirmar la ausencia de una transacción es estar al tanto de todas las transacciones. En el modelo basado en la casa de moneda, la casa de moneda estaba al tanto de todas las transacciones y decidía cuál llegaba primero. Para lograr esto sin una parte confiable, las transacciones deben anunciarse públicamente [1] y necesitamos un sistema para que los participantes acuerden un historial único del orden en que fueron recibidas. El beneficiario necesita prueba de que en el momento de cada transacción, la mayoría de los nodos acordaron que fue el primero en recibirse.
3. Servidor de marca de tiempo
La solución que proponemos comienza con un servidor de marca de tiempo. Un servidor de marca de tiempo funciona tomando un hash de un bloque de elementos a los que se les debe poner una marca de tiempo y publicando ampliamente el hash, como en un periódico o en una publicación de Usenet [2-5]. La marca de tiempo demuestra que los datos deben haber existido en ese momento, obviamente, para poder ingresar al hash. Cada marca de tiempo incluye la marca de tiempo anterior en su hash, formando una cadena, y cada marca de tiempo adicional refuerza las anteriores.

4. Prueba de trabajo
Para implementar un servidor de marca de tiempo distribuido de igual a igual, necesitaremos utilizar un sistema de prueba de trabajo similar al Hashcash de Adam Back [6], en lugar de publicaciones de periódicos o Usenet. La prueba de trabajo implica buscar un valor que, cuando se aplica un hash, como con SHA-256, el hash comienza con una cantidad de bits cero. El trabajo promedio requerido es exponencial en la cantidad de bits cero requeridos y se puede verificar ejecutando un único hash.
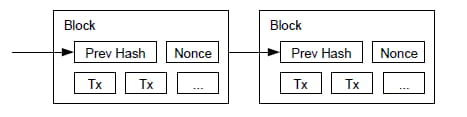
Para nuestra red de marca de tiempo, implementamos la prueba de trabajo incrementando un nonce en el bloque hasta que se encuentra un valor que le da al hash del bloque los cero bits requeridos. Una vez que se ha invertido el esfuerzo de la CPU para satisfacer la prueba de trabajo, el bloque no se puede cambiar sin rehacer el trabajo. Como los bloques posteriores se encadenan después de él, el trabajo para cambiar el bloque incluiría rehacer todos los bloques posteriores.
La prueba de trabajo también resuelve el problema de determinar la representación en la toma de decisiones por mayoría. Si la mayoría se basara en una dirección IP, un voto, cualquiera que pudiera asignar muchas IP podría subvertirla. La prueba de trabajo es esencialmente una CPU, un voto. La decisión mayoritaria está representada por la cadena más larga, que tiene el mayor esfuerzo de prueba de trabajo invertido en ella. Si la mayor parte de la potencia de la CPU está controlada por nodos honestos, la cadena honesta crecerá más rápido y superará a cualquier cadena competidora. Para modificar un bloque anterior, un atacante tendría que rehacer la prueba de trabajo del bloque y todos los bloques posteriores y luego alcanzar y superar el trabajo de los nodos honestos. Más adelante mostraremos que la probabilidad de que un atacante más lento se ponga al día disminuye exponencialmente a medida que se agregan bloques posteriores.
Para compensar el aumento de la velocidad del hardware y el interés variable en ejecutar nodos a lo largo del tiempo, la dificultad de la prueba de trabajo está determinada por un promedio móvil dirigido a una cantidad promedio de bloques por hora. Si se generan demasiado rápido, la dificultad aumenta.
5. Red
Los pasos para ejecutar la red son los siguientes:
1) Las nuevas transacciones se transmiten a todos los nodos.
2) Cada nodo recopila nuevas transacciones en un bloque.
3) Cada nodo trabaja para encontrar una prueba de trabajo difícil para su bloque.
4) Cuando un nodo encuentra prueba de trabajo, transmite el bloque a todos los nodos.
5) Los nodos aceptan el bloque solo si todas las transacciones que contiene son válidas y aún no se han gastado.
6) Los nodos expresan su aceptación del bloque trabajando en la creación del siguiente bloque de la cadena, utilizando el hash del bloque aceptado como hash anterior.
Los nodos siempre consideran que la cadena más larga es la correcta y seguirán trabajando para extenderla. Si dos nodos transmiten diferentes versiones del siguiente bloque simultáneamente, algunos nodos pueden recibir uno u otro primero. En ese caso, trabajan en la primera que recibieron, pero guardan la otra rama en caso de que se alargue. El empate se romperá cuando se encuentre la siguiente prueba de trabajo y una rama se alargue; los nodos que estaban trabajando en la otra rama cambiarán a la más larga.
No es necesario que las transmisiones de nuevas transacciones lleguen a todos los nodos. Siempre que lleguen a muchos nodos, pronto entrarán en un bloque. Las transmisiones en bloque también toleran la caída de mensajes. Si un nodo no recibe un bloque, lo solicitará cuando reciba el siguiente bloque y se dé cuenta de que ha perdido uno.
6. Incentivo
Por convención, la primera transacción en un bloque es una transacción especial que inicia una nueva moneda propiedad del creador del bloque. Esto agrega un incentivo para que los nodos apoyen la red y proporciona una forma de distribuir inicialmente monedas en circulación, ya que no existe una autoridad central para emitirlas. La adición constante de una cantidad constante de nuevas monedas es análoga a que los mineros de oro gasten recursos para agregar oro a la circulación. En nuestro caso, lo que se gasta es tiempo de CPU y electricidad.
El incentivo también se puede financiar con tarifas de transacción. Si el valor de salida de una transacción es menor que su valor de entrada, la diferencia es una tarifa de transacción que se agrega al valor del incentivo del bloque que contiene la transacción. Una vez que una cantidad predeterminada de monedas ha entrado en circulación, el incentivo puede pasar por completo a tarifas de transacción y estar completamente libre de inflación.
El incentivo puede ayudar a alentar a los nodos a ser honestos. Si un atacante codicioso es capaz de reunir más potencia de CPU que todos los nodos honestos, tendría que elegir entre usarla para defraudar a la gente robándole sus pagos o usarla para generar nuevas monedas. Debería encontrarle más rentable seguir las reglas, reglas que le favorecen con más monedas nuevas que a todos los demás juntos, que socavar el sistema y la validez de su propia riqueza.
7. Recuperar espacio en disco
Una vez que la última transacción en una moneda está enterrada bajo suficientes bloques, las transacciones gastadas antes se pueden descartar para ahorrar espacio en el disco. Para facilitar esto sin romper el hash del bloque, las transacciones se procesan en un árbol Merkle [7][2][5], con solo la raíz incluida en el hash del bloque. Luego, los bloques viejos se pueden compactar cortando ramas del árbol. No es necesario almacenar los hashes interiores.

Un encabezado de bloque sin transacciones tendría aproximadamente 80 bytes. Si suponemos que los bloques se generan cada 10 minutos, 80 bytes 6 24 * 365 = 4,2 MB por año. Dado que los sistemas informáticos se venden normalmente con 2 GB de RAM en 2008, y la Ley de Moore predice un crecimiento actual de 1,2 GB por año, el almacenamiento no debería ser un problema incluso si los encabezados de los bloques deben mantenerse en la memoria.
8. Verificación de pago simplificada
Es posible verificar pagos sin ejecutar un nodo de red completo. Un usuario solo necesita conservar una copia de los encabezados de bloque de la cadena de prueba de trabajo más larga, que puede obtener consultando los nodos de la red hasta que esté convencido de que tiene la cadena más larga, y obtener la rama de Merkle que vincula la transacción al bloque. tiene marca de tiempo. No puede verificar la transacción por sí mismo, pero al vincularla a un lugar en la cadena, puede ver que un nodo de la red la ha aceptado y los bloques agregados después de confirmar que la red la ha aceptado.

Como tal, la verificación es confiable siempre que nodos honestos controlen la red, pero es más vulnerable si la red es dominada por un atacante. Si bien los nodos de la red pueden verificar las transacciones por sí mismos, el método simplificado puede ser engañado por transacciones fabricadas por un atacante mientras el atacante pueda continuar dominando la red. Una estrategia para protegerse contra esto sería aceptar alertas de los nodos de la red cuando detecten un bloque no válido, solicitando al software del usuario que descargue el bloque completo y alertando a las transacciones para confirmar la inconsistencia. Las empresas que reciben pagos frecuentes probablemente seguirán queriendo ejecutar sus propios nodos para obtener una seguridad más independiente y una verificación más rápida.
9. Combinar y dividir valor
Aunque sería posible manejar monedas individualmente, sería difícil realizar una transacción separada por cada centavo de una transferencia. Para permitir dividir y combinar el valor, las transacciones contienen múltiples entradas y salidas. Normalmente habrá una única entrada de una transacción anterior más grande o múltiples entradas que combinan cantidades más pequeñas, y como máximo dos salidas: una para el pago y otra para devolver el cambio, si lo hubiera, al remitente.

Cabe señalar que el despliegue, donde una transacción depende de varias transacciones, y esas transacciones dependen de muchas más, no es un problema aquí. Nunca es necesario extraer una copia independiente completa del historial de una transacción.
10. Privacidad
El modelo bancario tradicional logra un nivel de privacidad al limitar el acceso a la información a las partes involucradas y al tercero de confianza. La necesidad de anunciar públicamente todas las transacciones impide este método, pero aún se puede mantener la privacidad interrumpiendo el flujo de información en otro lugar: manteniendo las claves públicas en el anonimato. El público puede ver que alguien está enviando una cantidad a otra persona, pero sin información que vincule la transacción con nadie. Esto es similar al nivel de información publicada por las bolsas de valores, donde el momento y el tamaño de las operaciones individuales, la "cinta", se hacen públicos, pero sin decir quiénes fueron las partes.

Como firewall adicional, se debe utilizar un nuevo par de claves para cada transacción para evitar que se vinculen a un propietario común. Algunos vínculos siguen siendo inevitables en el caso de transacciones con múltiples insumos, que necesariamente revelan que sus insumos pertenecían al mismo propietario. El riesgo es que si se revela el propietario de una clave, la vinculación podría revelar otras transacciones que pertenecieron al mismo propietario.
11. Cálculos
Consideramos el escenario de un atacante que intenta generar una cadena alternativa más rápido que la cadena honesta. Incluso si esto se logra, no deja al sistema expuesto a cambios arbitrarios, como crear valor de la nada o tomar dinero que nunca perteneció al atacante. Los nodos no aceptarán una transacción no válida como pago, y los nodos honestos nunca aceptarán un bloque que las contenga. Un atacante sólo puede intentar cambiar una de sus propias transacciones para recuperar el dinero que gastó recientemente. La carrera entre la cadena honesta y la cadena atacante se puede caracterizar como una caminata aleatoria binomial. El evento de éxito es que la cadena honesta se extiende en un bloque, lo que aumenta su ventaja en +1, y el evento de fracaso es que la cadena del atacante se extiende en un bloque, lo que reduce la brecha en -1.
La probabilidad de que un atacante se recupere de un déficit determinado es análoga al problema de la ruina del jugador. Supongamos que un jugador con crédito ilimitado comienza con un déficit y juega potencialmente un número infinito de pruebas para intentar alcanzar el punto de equilibrio. Podemos calcular la probabilidad de que alguna vez alcance el punto de equilibrio, o de que un atacante alguna vez alcance la cadena honesta, de la siguiente manera [8]:
p = probabilidad de que un nodo honesto encuentre el siguiente bloque
q = probabilidad de que el atacante encuentre el siguiente bloque
qz = probabilidad de que el atacante alguna vez lo alcance desde z bloques detrás
qz= { 1 si p≤q
(q/p)^z si p>q}
Dada nuestra suposición de que p > q, la probabilidad cae exponencialmente a medida que aumenta el número de bloques que el atacante tiene que alcanzar. Con las probabilidades en su contra, si no da un paso adelante afortunado desde el principio, sus posibilidades se vuelven cada vez más pequeñas a medida que se queda más atrás.
Ahora consideramos cuánto tiempo debe esperar el destinatario de una nueva transacción antes de estar suficientemente seguro de que el remitente no puede cambiar la transacción. Suponemos que el remitente es un atacante que quiere hacer creer al destinatario que le pagó por un tiempo y luego cambiarlo para que se pague a sí mismo después de que haya pasado un tiempo. El receptor será alertado cuando eso suceda, pero el remitente espera que sea demasiado tarde.
El receptor genera un nuevo par de claves y entrega la clave pública al remitente poco antes de firmar. Esto evita que el remitente prepare una cadena de bloques con anticipación trabajando en ella continuamente hasta que tenga la suerte de avanzar lo suficiente y luego ejecute la transacción en ese momento. Una vez enviada la transacción, el remitente deshonesto comienza a trabajar en secreto en una cadena paralela que contiene una versión alternativa de su transacción.
El destinatario espera hasta que la transacción se haya agregado a un bloque y se hayan vinculado z bloques después. No sabe la cantidad exacta de progreso que ha logrado el atacante, pero suponiendo que los bloques honestos tomaron el tiempo promedio esperado por bloque, el progreso potencial del atacante será una distribución de Poisson con valor esperado:

Convirtiendo a código C...

Al ejecutar algunos resultados, podemos ver que la probabilidad cae exponencialmente con z.
q=0,1
z=0P=1.0000000
z=1 P=0,2045873
z=2 P=0,0509779
z=3 P=0,0131722
z=4 P=0,0034552
z=5 P=0,0009137
z=6 P=0,0002428
z=7 P=0,0000647
z=8P=0.0000173
z=9P=0.0000046
z=10 P=0,0000012
q=0,3
z=0P=1.0000000
z=5 P=0,1773523
z=10 P=0,0416605
z=15 P=0,0101008
z=20 P=0,0024804
z=25 P=0,0006132
z=30 P=0,0001522
z=35 P=0,0000379
z=40 P=0,0000095
z=45 P=0,0000024
z=50 P=0,0000006
Resolviendo para P menor que 0.1%...
P < 0,001
q=0,10z=5
q=0,15z=8
q=0,20z=11
q=0,25z=15
q=0,30z=24
q=0,35z=41
q=0,40z=89
q=0,45z=340
12. Conclusión
Hemos propuesto un sistema para transacciones electrónicas sin depender de la confianza. Comenzamos con el marco habitual de monedas elaboradas a partir de firmas digitales, que proporciona un fuerte control de la propiedad, pero está incompleto sin una forma de evitar el doble gasto. Para resolver esto, propusimos una red peer-to-peer que utiliza prueba de trabajo para registrar un historial público de transacciones que rápidamente se vuelve impracticable desde el punto de vista computacional para que un atacante lo cambie si los nodos honestos controlan la mayor parte de la potencia de la CPU. La red es robusta en su simplicidad no estructurada. Los nodos funcionan todos a la vez con poca coordinación. No es necesario identificarlos, ya que los mensajes no se enrutan a ningún lugar en particular y sólo deben entregarse con el mejor esfuerzo posible. Los nodos pueden salir y volver a unirse a la red a voluntad, aceptando la cadena de prueba de trabajo como prueba de lo que sucedió mientras no estaban. Votan con la potencia de su CPU, expresando su aceptación de bloques válidos trabajando para extenderlos y rechazando bloques no válidos negándose a trabajar en ellos. Cualquier regla e incentivo necesarios se puede hacer cumplir con este mecanismo de consenso.
Referencias
[1] W. Dai, "b-money", http://www.weidai.com/bmoney.txt, 1998.
[2] H. Massías, XS. Ávila y J.-J. Quisquater, "Diseño de un servicio de sellado de tiempo seguro con mínimo
requisitos de confianza", en el 20º Simposio sobre Teoría de la Información en el Benelux, mayo de 1999.
[3] S. Haber, W.S. Stornetta, "Cómo sellar la hora de un documento digital", en Journal of Cryptology, vol 3, no
2, páginas 99-111, 1991.
[4] D. Bayer, S. Haber, W.S. Stornetta, "Mejora de la eficiencia y confiabilidad del sellado de tiempo digital",
En Secuencias II: Métodos en comunicación, seguridad e informática, páginas 329-334, 1993.
[5] S. Haber, W.S. Stornetta, "Nombres seguros para cadenas de bits", en actas de la cuarta conferencia ACM
sobre seguridad informática y de las comunicaciones, páginas 28-35, abril de 1997.
[6] A. Atrás, "Hashcash: una contramedida de denegación de servicio",
http://www.hashcash.org/papers/hashcash.pdf, 2002.
[7] RC Merkle, "Protocolos para criptosistemas de clave pública", en Proc. 1980 Simposio sobre Seguridad y
Privacidad, IEEE Computer Society, páginas 122-133, abril de 1980.
[8] W. Feller, "Una introducción a la teoría de la probabilidad y sus aplicaciones", 1957.



