In modern financial theory, evaluating investment performance often extends beyond the traditional analysis of mean return and standard deviation. While established metrics such as the Sharpe Ratio rely on the assumption of a normal distribution of returns, real-world market data—particularly for digital assets like Bitcoin (BTC)—frequently exhibit asymmetry and "fat tails." The Omega Ratio offers a fundamentally different approach by utilizing the entire cumulative distribution of returns to distinguish profit potential from the risk of loss relative to a defined threshold.
1. Definition and Mathematical Foundation
According to the research of Kapsos et al. (2011), the Omega Ratio allows analysts to evaluate the probability of achieving a specific target return by integrating the entire probability density. The ratio is defined as the relationship between probability-weighted gains and probability-weighted losses at a Minimum Acceptable Return (MAR) threshold.
The mathematical representation of Omega (Ω) is derived via the Cumulative Distribution Function (CDF):
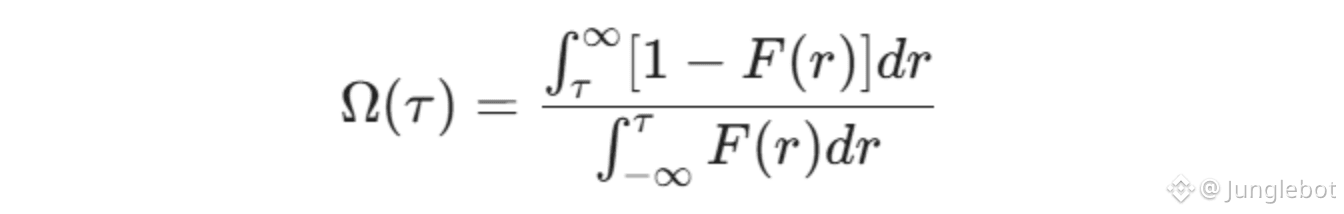
Where:
Ω: The Omega Ratio.
𝞃 (tau): The Minimum Acceptable Return (MAR) threshold defined by the investor.
F(r): The Cumulative Distribution Function (CDF) of the asset's returns.
r: The asset's return.
Through integration by parts, the equation can be presented in a more computationally applicable form based on expected values. This determines the mass of the return distribution above the threshold [𝞃, +∞] (positive return relative to 𝞃) and below the threshold [-∞, 𝞃] (negative return relative to 𝞃):
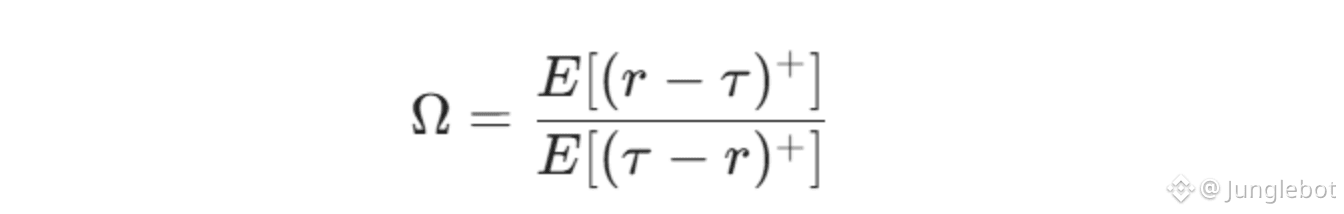
Where:
E[(r - 𝞃)+]: The expected value of gains above threshold 𝞃.
E[(𝞃 - r)+]: The expected value of losses below threshold 𝞃.
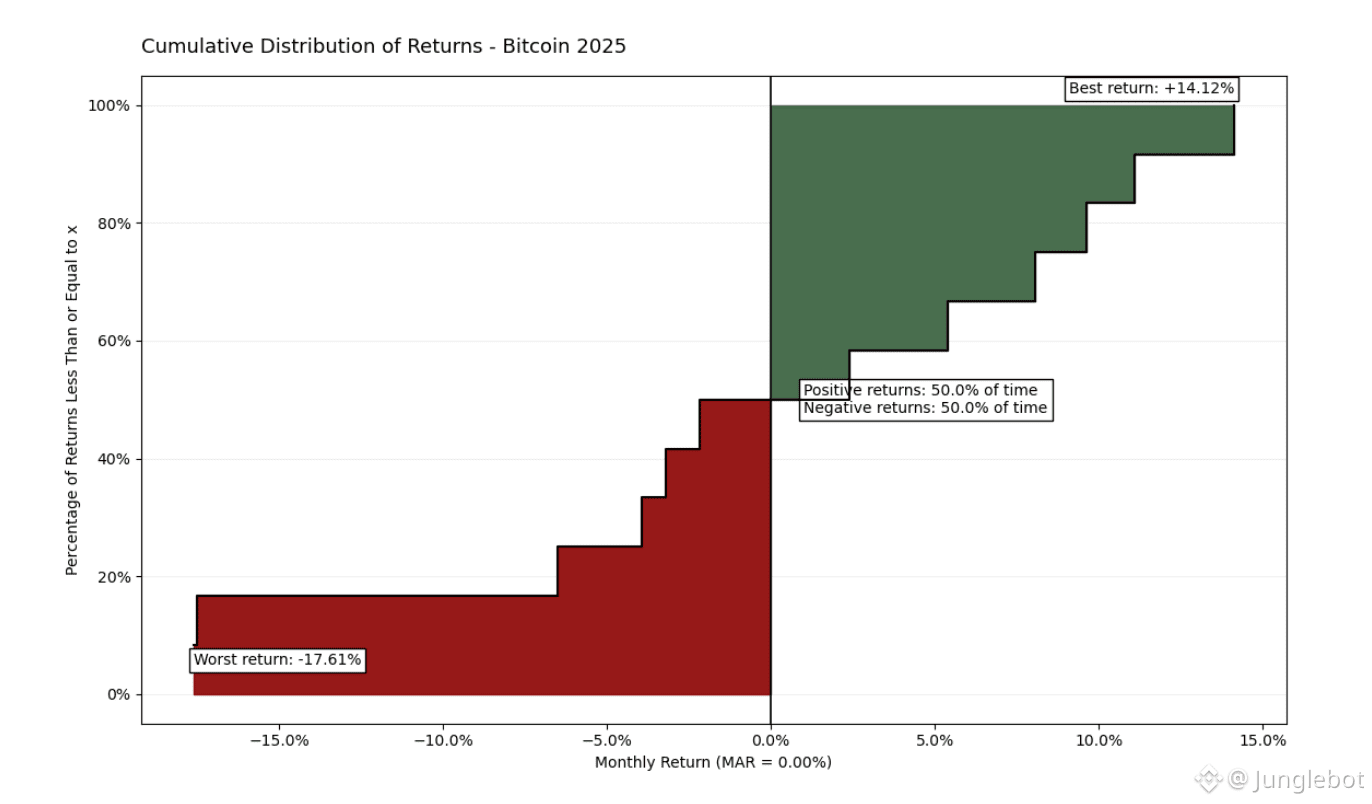
The 2025 data illustrates the asset's asymmetric volatility, with extreme fluctuations ranging between -17.61% and +14.12%. Despite a balanced frequency (50% positive vs. 50% negative months), an Omega Ratio of 0.778 reveals a heavier weight of losses in the left tail of the curve. This visual parity emphasizes that the magnitude of drawdowns dominates the rallies, serving as a fundamental basis for assessing asset quality relative to the chosen MAR.
While a one-year chart may seem bulky and less informative, expanding the time horizon to a 10-year period provides a significantly more comprehensive picture.
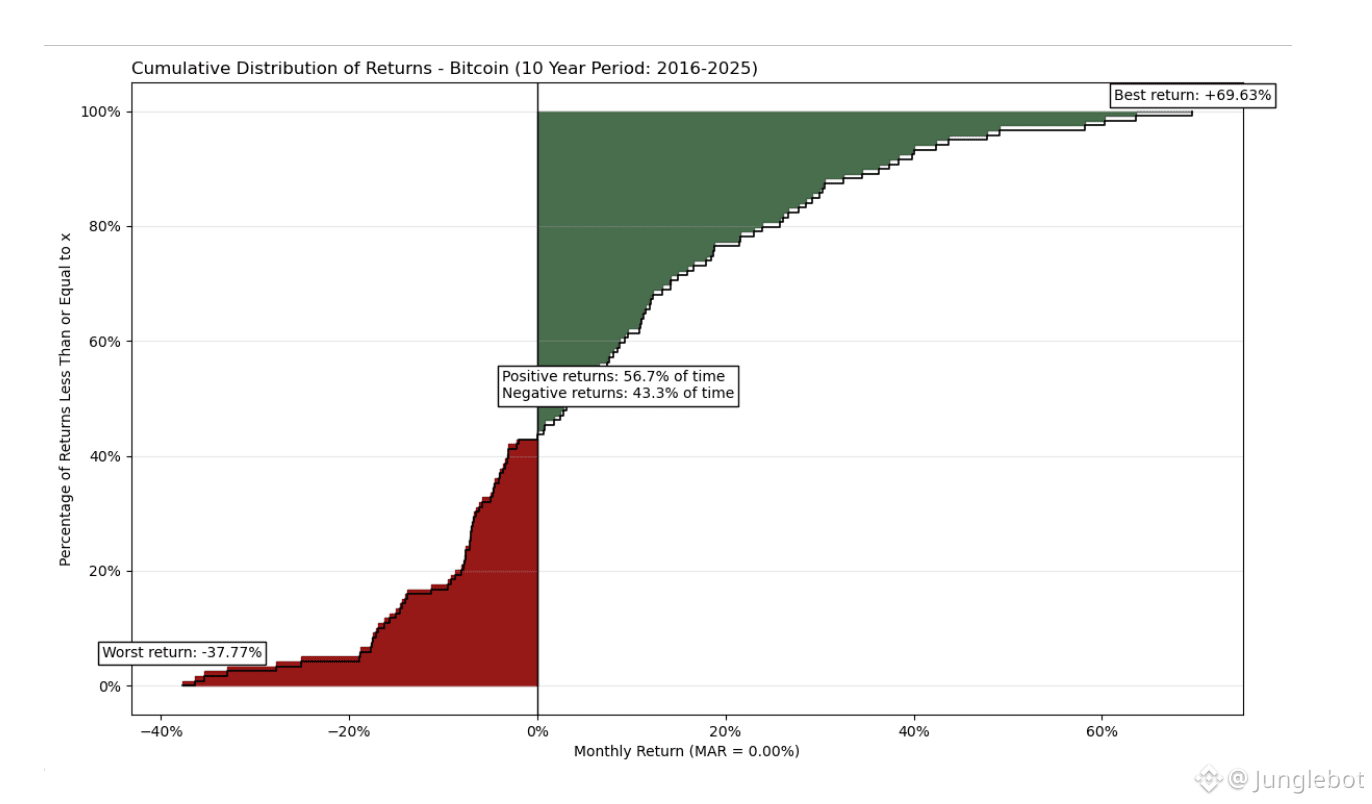
The 10-year analysis reveals a much more favorable risk-return profile. Although the asset retains extreme volatility with monthly drawdowns as low as -37.77%, it demonstrates impressive growth potential with peaks up to +69.63%. Unlike the one-year snapshot, positive months dominate here (56.7% of the time), and the "green zone" of profit visually and mathematically outweighs the "red zone" of risk. The Omega Ratio for this period is 1.621, proving that Bitcoin generates a significant premium relative to the risk taken over the long term.
2. Interpretation and Risk Analysis
Unlike other coefficients, the value of Omega depends directly on the chosen threshold 𝞃. This makes the metric adaptive to the investor's specific risk profile.
Ω > 1: Indicates that the cumulative value of gains exceeds that of losses relative to the chosen MAR. A higher number signifies better quality of returns.
Ω = 1: Means the asset's expected return is exactly equal to the threshold 𝞃.
Ω < 1: Signals that the risk of loss below the chosen "bar" outweighs the potential for gain.
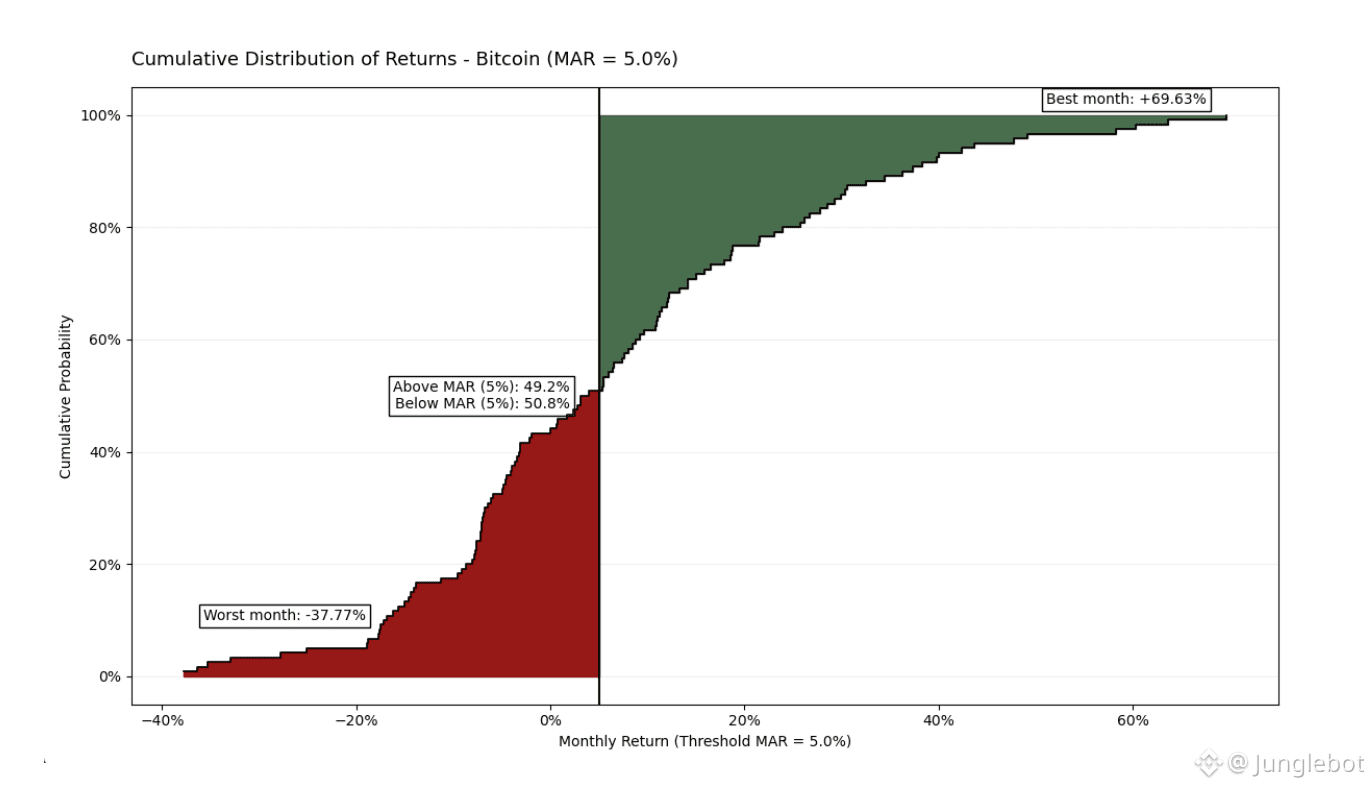
In the analyzed 10-year period, applying a MAR of 5% monthly places the asset in a stricter framework. Although Bitcoin remains below this threshold 50.8% of the time, its Omega Ratio remains positive at 1.2102. This confirms that the contribution of "explosive" months (reaching up to +69.63%) is powerful enough to outweigh the cumulative effect of months with negative or mediocre returns. The data proves that even under high investment expectations, Bitcoin maintains its statistical advantage in the long run.
3. Optimization via Linear Programming
One of the most significant practical applications of the Omega Ratio, detailed by Kapsos et al. (2011), is its use in active portfolio construction. While the function may initially appear complex to calculate, the authors prove that maximizing Omega can be reformulated as a linear programming problem.
The discrete analog of Omega for computational purposes over $m$ historical observations is:
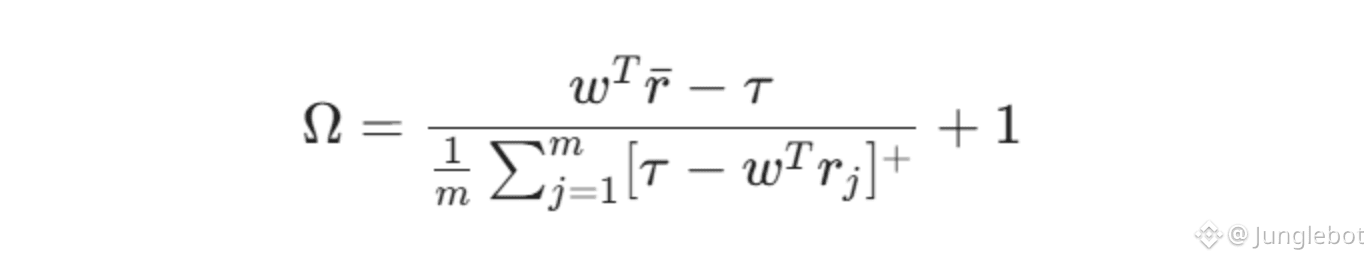
Where:
𝑤: Vector of asset weights in the portfolio.
r: Vector of mean historical returns.
m: Number of historical observations (samples).
rj: Vector of returns for each specific observation ⅉ.
This approach is fundamentally different from traditional Markowitz (Mean-Variance) optimization. Instead of simply minimizing volatility (which penalizes sharp upward moves), the Omega model allows Bitcoin investors to optimize their positions to maximize the "upper tail" of the distribution. By adding one to the ratio of net excess return to mean shortfall, the Kapsos formula allows algorithms to quickly and efficiently find the weights (𝑤) that offer the best probability of success relative to individual investor goals.
4. Comparative Analysis: Bitcoin vs. S&P 500
To understand the true value of the Omega Ratio, it is necessary to compare Bitcoin against a traditional benchmark like the S&P 500 index. Traditional risk metrics like standard deviation often fail here because they do not account for the asymmetry and differences in the "tail" structures of the two distributions.
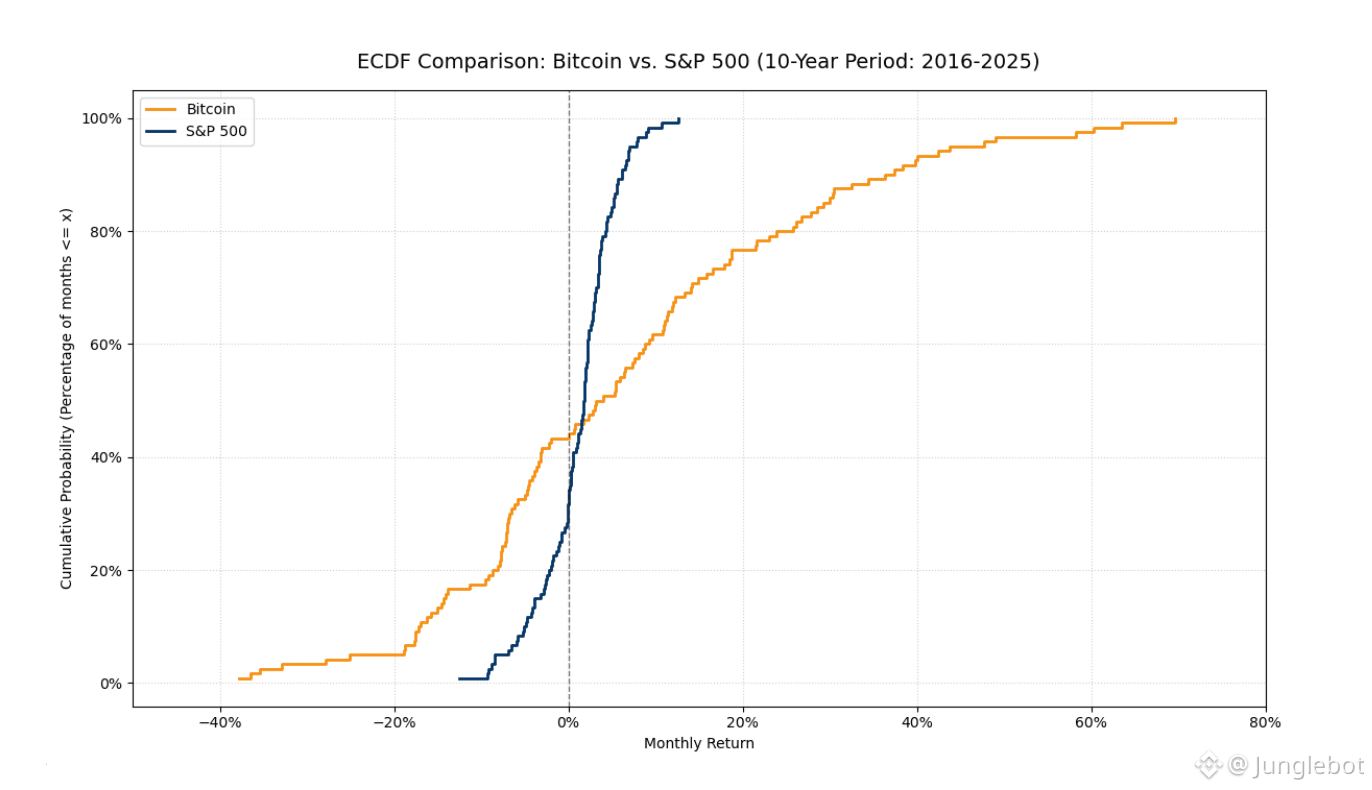
This comparative ECDF plot illustrates the fundamental difference between the two assets:
Concentration vs. Volatility: The S&P 500 line (dark blue) is significantly steeper and concentrated in a narrow range around zero. This indicates an asset with lower volatility and a tighter, more predictable distribution.
Bitcoin's "Fat Tails": The Bitcoin line (orange) demonstrates significantly wider extremes. This is visual evidence of "fat tails"—a higher probability of massive negative and positive deviations compared to the traditional market.
Performance Specifics: While Bitcoin's worst month reached -37.77%, the asset successfully generated explosive growth periods of up to +69.63%. These asymmetric jumps in the "right tail" are why Bitcoin often generates a much higher Omega Ratio at lower MAR levels.
Conclusion: The comparison confirms that Omega is a fairer risk metric than standard deviation. It recognizes Bitcoin's high potential without ignoring its "fat tail" characteristics, while allowing investors to apply the optimization formula to balance portfolio weights (𝑤) against a desired return threshold (𝞃).
Final Conclusion
Analysis via the Omega Ratio proves that traditional metrics like the Sharpe Ratio are insufficient for assets with "fat tails" like Bitcoin. While a one-year period can be misleading, the 10-year horizon reveals the statistical dominance of gains (Ω = 1.621). Even at a high threshold of MAR = 5%, the asset maintains its efficiency (Ω = 1.2102) due to the magnitude of its positive outliers. The comparison with the S&P 500 highlights that Bitcoin offers unique exposure to the "right tail" of the distribution. Utilizing the Kapsos et al. model transforms these theoretical insights into a practical tool for portfolio optimization via linear programming. Ultimately, the Omega Ratio provides a more honest and adaptive assessment of risk, acknowledging the potential for explosive growth.
References
Kapsos, M., Zymler, S., Christofides, N., and Rustem, B. (2011). Optimizing the Omega Ratio using Linear Programming. Imperial College London.
